Kate Haitsiukevich

I am a PhD student at Aalto University School of Science supervised by Prof. Pekka Marttinen and advised by Dr. Alexander Ilin.

I am passionate about deep learning methods for science and engineering. My research focuses on making developing sample-efficient methods for modeling of physical systems. Prior to starting my PhD studies I've worked as a Data Scientist and a Quantitative Analyst in the financial industry. I've earned my Bachelor's and Master's degrees in Applied Mathematics. My framework of choice is Pytorch 🔥.

Email / CV / Google Scholar / Github

Research

I study the ways to efficiently incorporate the prior knowledge about the system, often expressed as Partial Differential Equations (PDEs), into neural network architectures and training procedures for systems modeling.

PDEs are the established mathematical models for many real-world problems. However, only a handful of them have an analytical solution while for the rest the solution is approximated numerically. Traditional numerical solvers usually provide an accurate approximation that can be used to augment the training dataset but on its own they tend to be quite slow and inefficient. Other limitation of traditional techniques is their inability to seamlessly incorporate observations from the real process into the modeling.

Alternatively, neural network-based algorithms are data-driven in nature and have faster inference but usually require significant data collection for training which may not be available. Enhancing latest advances in deep learning with the knowledge of the underlying equation and the right set of inductive biases results in a hybrid model applicable for challenging data scarce regime. Such hybrid models usually better capture the underlying physics of the proses and improve the results.

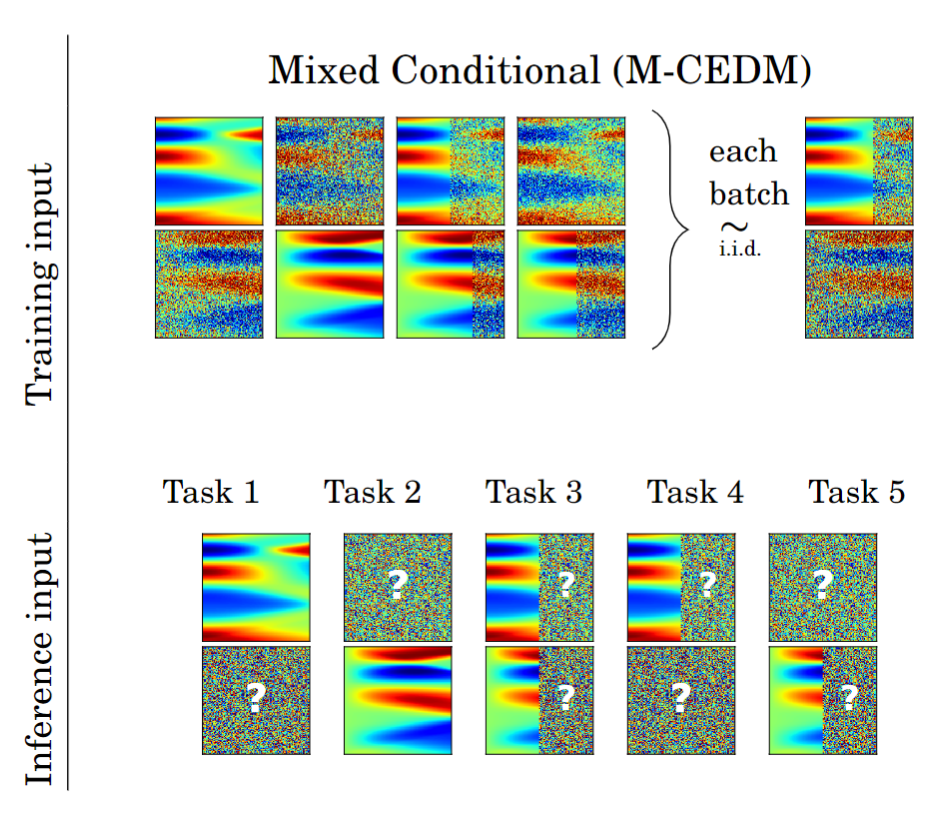
	Diffusion models as probabilistic neural operators for recovering unobserved states of dynamical systems Katsiaryna Haitsiukevich, Onur Poyraz, Pekka Marttinen, Alexander Ilin IEEE 34th International Workshop on Machine Learning for Signal Processing (MLSP), 2024 arXiv / Code / BibTex A diffusion-based surrogate model for PDE simulations trained for mixed conditional setting of forward (to predict the solution from parameters) and inverse problems (to recover unobserved states or parameter values).
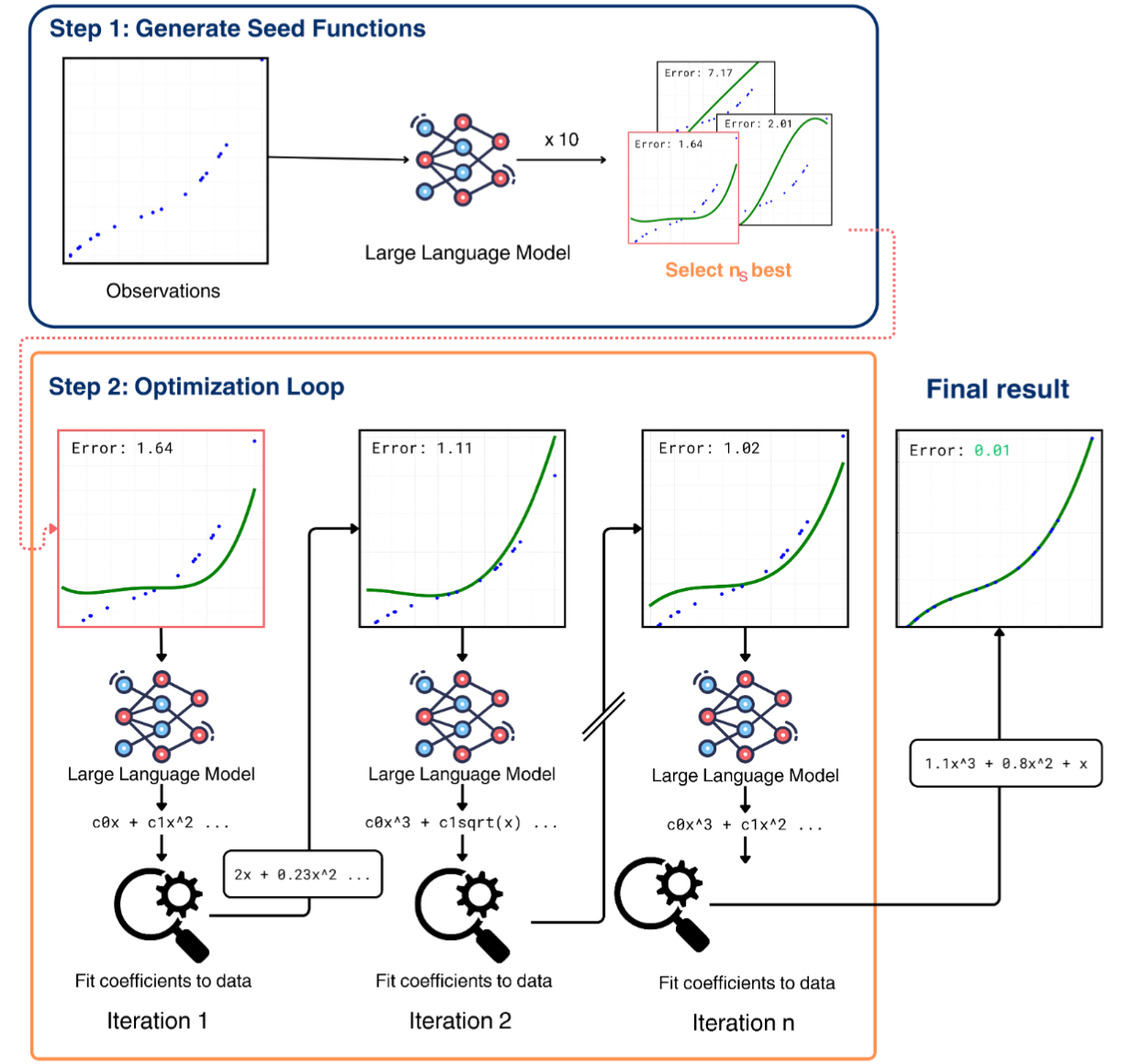
	In-Context Symbolic Regression: Leveraging Large Language Models for Function Discovery Matteo Merler, Katsiaryna Haitsiukevich, Nicola Dainese, Pekka Marttinen Association for Computational Linguistics 2024 Student Research Workshop* , 2024 arXiv / Code / BibTex A novel method for deriving analytical equation from the process measurements (symbolic regression) with an LLM pre-trained on natural language. The method consists of generation of a candidate function set and an iterative refinement procedure.
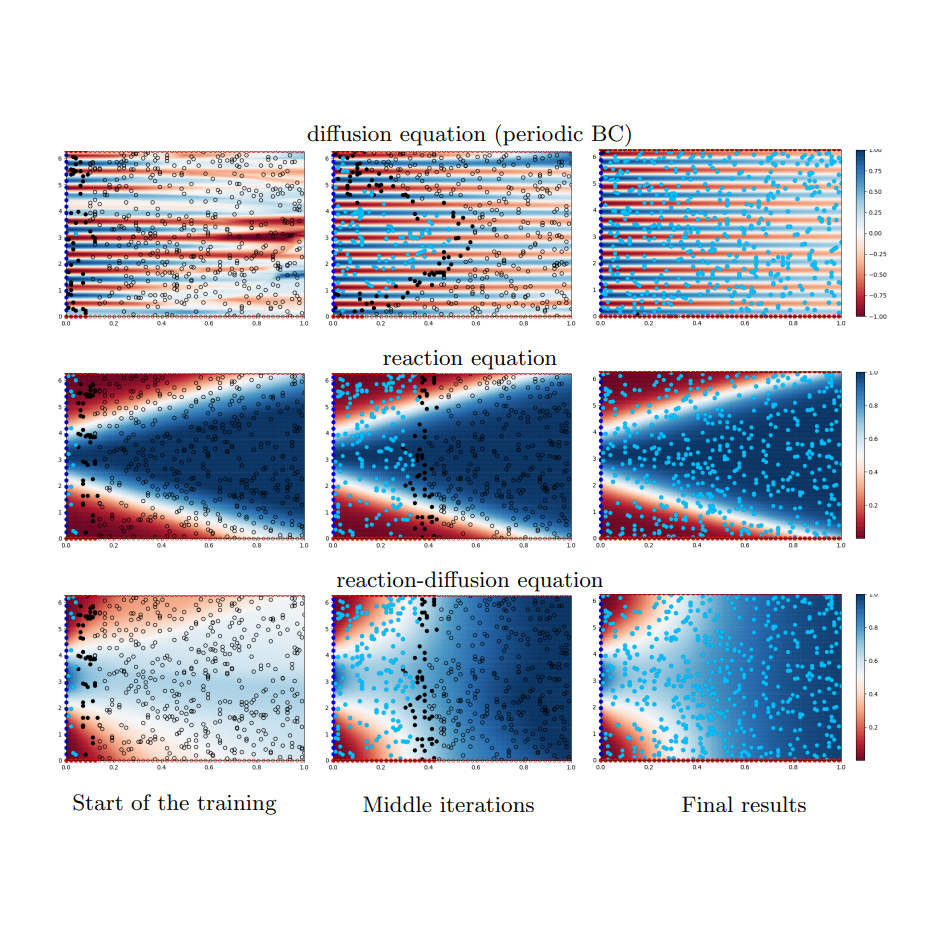
	Improved Training of Physics-Informed Neural Networks with Model Ensembles Katsiaryna Haitsiukevich, Alexander Ilin International Joint Conference on Neural Networks (IJCNN), 2023 arXiv / Code / BibTex Neural PDE solvers benefit from gradual expansion of the solution domain starting from points with supervision signal (e.g. initial conditions). We propose to automate this expansion based on the agreement of PDE solver ensemble.
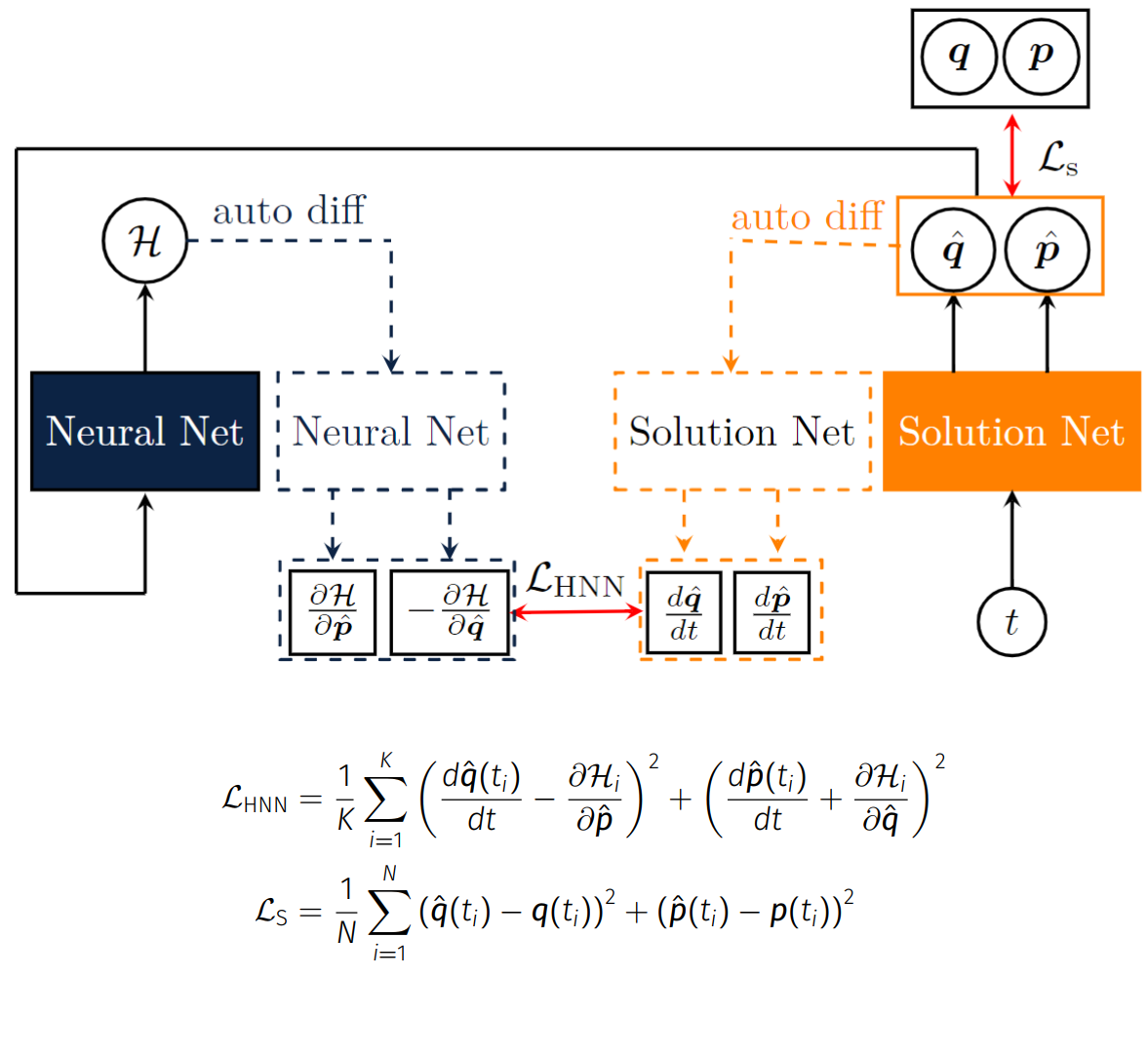
	Learning Trajectories of Hamiltonian Systems with Neural Networks Katsiaryna Haitsiukevich, Alexander Ilin Artificial Neural Networks and Machine Learning (ICANN), 2022 arXiv / BibTex A neural network architecture with encoded energy conservation inductive bias that enables direct calculation of the derivatives needed to satisfy the conservation constrains.
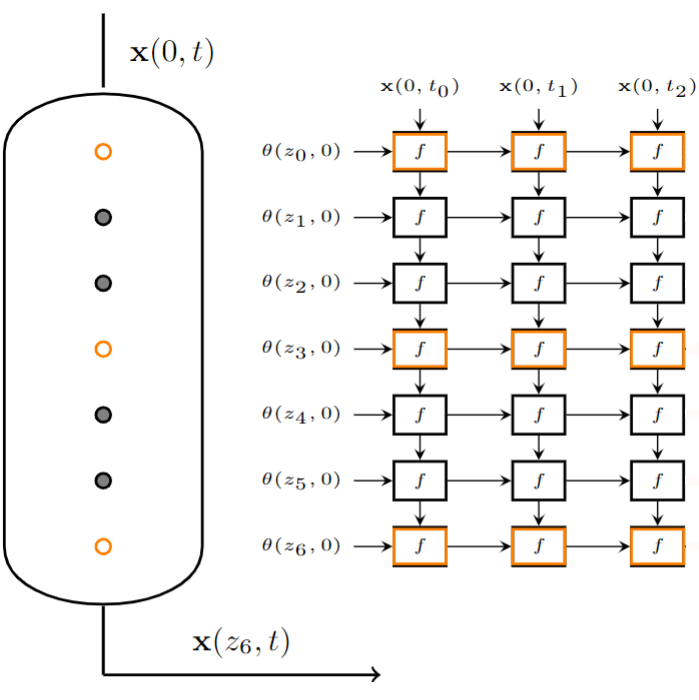
	A Deep Learning Model of Tubular Reactors Katsiaryna Haitsiukevich, Samuli Bergman, Cesar de Araujo Filho, Francesco Corona, Alexander Ilin IEEE 19th International Conference on Industrial Informatics (INDIN), 2021 arXiv / BibTex We developed a PDE-motivated neural network architecture for modeling tubular reactor states. The project was done in collaboration with Neste.

Teaching

During my studies I advised the following research projects and theses:

Master’s thesis “Transformer? Improving training of Physics-Informed Neural Nets”, 2024
Bachelor’s thesis "Physics-informed neural networks: accuracy and convergence", 2024
Bachelor’s thesis "Latest Breakthrough in Diffusion Model and its Applications", 2024
Research project ”Equivariant physics-informed neural networks”, 2023
Research project ”Simulating a reactor with neural networks”, 2021

I participated as a Teaching Assistant in the following courses:

Webpage design courtesy of Jon Barron.